Diferencia entre revisiones de «CAFE-Pendulos en sincronia»
(→Péndulos en sincronía) |
|||
| (No se muestran 3 ediciones intermedias del mismo usuario) | |||
| Línea 4: | Línea 4: | ||
El sistema que usted está observando se construyó en base a 14 péndulos con diferentes longitudes. El período de un péndulo, <math>\tau</math>, está determinado por su longitud, <math>\ell</math>, y la aceleración de la gravedad, <math>g</math>, a través de la siguiente relación<br> | El sistema que usted está observando se construyó en base a 14 péndulos con diferentes longitudes. El período de un péndulo, <math>\tau</math>, está determinado por su longitud, <math>\ell</math>, y la aceleración de la gravedad, <math>g</math>, a través de la siguiente relación<br> | ||
| + | <div style="text-align:center;"> | ||
<math>\tau = 2 \pi \sqrt {\frac \ell g}</math><br> | <math>\tau = 2 \pi \sqrt {\frac \ell g}</math><br> | ||
| + | </div> | ||
En Bariloche, a 893 m por encima del nivel del mar y a 41<math>^o</math>09' de latitud sur, la aceleración de la gravedad vale muy aproximadamente <math>g = 9.8 \, \textrm{m} / \textrm{s}^2</math>. | En Bariloche, a 893 m por encima del nivel del mar y a 41<math>^o</math>09' de latitud sur, la aceleración de la gravedad vale muy aproximadamente <math>g = 9.8 \, \textrm{m} / \textrm{s}^2</math>. | ||
| Línea 18: | Línea 20: | ||
Es importante hacer notar que el armazón donde están sujetos los péndulos es rígido, por lo cual la interacción entre ellos es casi inexistente, y se mueven de forma independiente. | Es importante hacer notar que el armazón donde están sujetos los péndulos es rígido, por lo cual la interacción entre ellos es casi inexistente, y se mueven de forma independiente. | ||
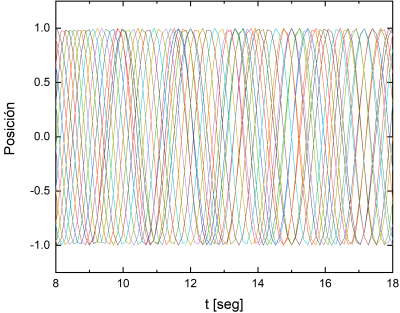
| − | Si se estudia el movimiento del conjunto de péndulos, en general se observa un movimiento aparentemente desordenado, como muestra el siguiente gráfico de las posiciones entre los 8 y 18 segundos | + | Si se estudia el movimiento del conjunto de péndulos, en general se observa un movimiento aparentemente desordenado, como muestra el siguiente gráfico de las posiciones de los 14 péndulos entre los 8 y 18 segundos |
[[File:8a18seg.png|center|400px]] | [[File:8a18seg.png|center|400px]] | ||
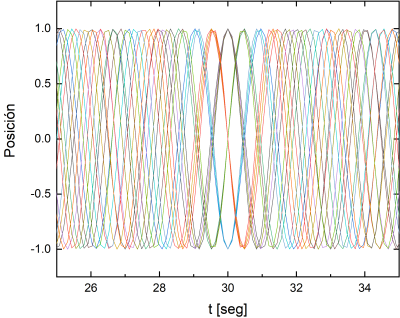
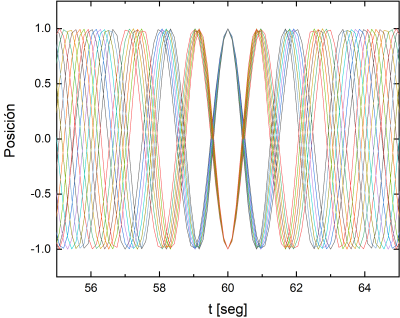
| − | Esto se debe a que los péndulos se mueven con diferentes períodos, y a medida que avanza el tiempo se van desfasando. Sin embargo, como los períodos no son al azar si no que fueron elegidos con la regla que cada péndulo hace media oscilación más que el péndulo anterior en 1 minuto, hay momentos donde los movimientos parecen relativamente coordinados, como muestran los siguientes gráficos entre 25 y 35 seg, y entre 55 y 65 segundos. | + | Esto se debe a que los péndulos se mueven con diferentes períodos, y a medida que avanza el tiempo se van desfasando. El siguiente video muestra lo que se observa, filmado en cámara rápida. |
| + | |||
| + | <div style="text-align:center;"> | ||
| + | <youtube width="200" height="347">2ZcyISgPoko</youtube> | ||
| + | </div> | ||
| + | |||
| + | Sin embargo, como los períodos no son al azar si no que fueron elegidos con la regla que cada péndulo hace media oscilación más que el péndulo anterior en 1 minuto, hay momentos donde los movimientos parecen relativamente coordinados, como se ve en el video y también muestran los siguientes gráficos entre 25 y 35 seg, y entre 55 y 65 segundos. | ||
[[File:25a35seg.png|400px]] [[File:55a65seg.png|400px]] | [[File:25a35seg.png|400px]] [[File:55a65seg.png|400px]] | ||
| Línea 33: | Línea 41: | ||
También existen instantes de aparente sincronía simétricos respecto a 60 segundos, a t = 72 s, t = 80 s, t = 90 s, t = 96 s y t = 100 s, iguales a los mostrados pero con las velocidades opuestas. | También existen instantes de aparente sincronía simétricos respecto a 60 segundos, a t = 72 s, t = 80 s, t = 90 s, t = 96 s y t = 100 s, iguales a los mostrados pero con las velocidades opuestas. | ||
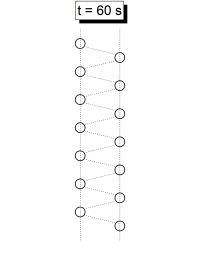
| − | Algunos de estos instantes son más fáciles de identificar que otros | + | Algunos de estos instantes son más fáciles de identificar que otros, como por ejemplo a t = 60 s, cuenado los péndulos se dividen en 2 grupos con velocidades opuestas. Los otros instantes de sincronía son mass difíciles de observar, ya que los péndulos se dividen en mas grupos y tienen velocidades opuestas. |
Revisión actual del 20:48 23 sep 2025
Péndulos en sincronía
El sistema que usted está observando se construyó en base a 14 péndulos con diferentes longitudes. El período de un péndulo, [math]\displaystyle{ \tau }[/math], está determinado por su longitud, [math]\displaystyle{ \ell }[/math], y la aceleración de la gravedad, [math]\displaystyle{ g }[/math], a través de la siguiente relación
[math]\displaystyle{ \tau = 2 \pi \sqrt {\frac \ell g} }[/math]
En Bariloche, a 893 m por encima del nivel del mar y a 41[math]\displaystyle{ ^o }[/math]09' de latitud sur, la aceleración de la gravedad vale muy aproximadamente [math]\displaystyle{ g = 9.8 \, \textrm{m} / \textrm{s}^2 }[/math].
El péndulo mas largo, el mas cercano a usted, tiene [math]\displaystyle{ \ell = 0.993 \textrm{m} }[/math] por lo cual su período vale [math]\displaystyle{ \tau = 2 \textrm{s} }[/math]. Es decir que realiza 30 oscilaciones en 1 minuto.
El segundo tiene una longitud un poco mas corta, de tal manera que el período es mas corto y realiza 30 oscilaciones y media en 1 minuto.
El tercero es aún mas corto y realiza 31 oscilaciones en 1 minuto.
Y así sucesivamente, hasta que el péndulo número 14, el último, realiza 36 oscilaciones y media en 1 minuto.
Es importante hacer notar que el armazón donde están sujetos los péndulos es rígido, por lo cual la interacción entre ellos es casi inexistente, y se mueven de forma independiente.
Si se estudia el movimiento del conjunto de péndulos, en general se observa un movimiento aparentemente desordenado, como muestra el siguiente gráfico de las posiciones de los 14 péndulos entre los 8 y 18 segundos
Esto se debe a que los péndulos se mueven con diferentes períodos, y a medida que avanza el tiempo se van desfasando. El siguiente video muestra lo que se observa, filmado en cámara rápida.
Sin embargo, como los períodos no son al azar si no que fueron elegidos con la regla que cada péndulo hace media oscilación más que el péndulo anterior en 1 minuto, hay momentos donde los movimientos parecen relativamente coordinados, como se ve en el video y también muestran los siguientes gráficos entre 25 y 35 seg, y entre 55 y 65 segundos.
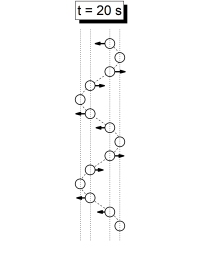
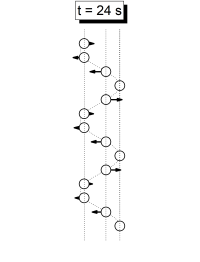
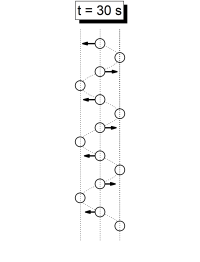
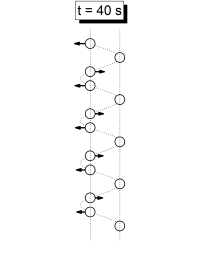
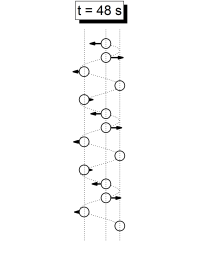
Se han identificado 6 momentos donde hay una aparente sincronía en el movimiento. Estos son t = 20 s, t = 24 s, t = 30 s, t = 40 s, t = 48 s y t= = 60 s. Los siguientes gráficos esquematizan las fotos del movimiento en esos instantes, con las flechas indicando las veolcidades, las lineas verticales mostrando los grupos en que se dividen los péndulos, y la linea ondulada mostrando la aparente onda que forman los péndulos.
También existen instantes de aparente sincronía simétricos respecto a 60 segundos, a t = 72 s, t = 80 s, t = 90 s, t = 96 s y t = 100 s, iguales a los mostrados pero con las velocidades opuestas.
Algunos de estos instantes son más fáciles de identificar que otros, como por ejemplo a t = 60 s, cuenado los péndulos se dividen en 2 grupos con velocidades opuestas. Los otros instantes de sincronía son mass difíciles de observar, ya que los péndulos se dividen en mas grupos y tienen velocidades opuestas.