CAFE-Modos normales

Modos normales (Péndulos acoplados)

Considere un sistema formado por varios componentes que presentan movimiento oscilatorio, y que incluye fuerzas de acoplamiento entre ellos. Debido a las fuerzas de acoplamiento no es posible mover un solo componente sin afectar a los demás.

El movimiento completo del sistema se describe usualmente en términos de modos normales, que son formas de oscilar de los componentes de tal manera que todos se mueven con la misma frecuencia. Nuevamente debido a las fuerzas de acoplamiento, esta frecuencia no necesariamente es la frecuencia de los componentes cuando no había interacción entre ellos.

Características importantes de los modos normales son:

• hay tantos como coordenadas describen el sistema.
• cualquier movimiento del sistema se puede describir como una superposición de ellos.
• son independientes entre sí, pudiendo moverse (evolucionar en el tiempo) sin interferencia.

Para investigar uno de estos sistemas y estudiar qué son los modos normales, se construyó un armazón cuadrado donde en cada brazo se colgó 1 péndulo. Se colgaron con tanza en forma de V de tal manera de impedir los movimientos laterales, permitiendo el movimiento solo hacia el centro del arreglo. Estos 4 péndulos, inicialmente independientes, se acoplaron sujetando un brazo rígido de plástico (un sorbete) entre los brazos aledaños de la V de tanza de los péndulos vecinos. Todos los acoplamientos se hicieron a la misma altura, 34 cm desde el borde superior de la tanza, medidos a lo largo de la tanza, no verticalmente. Previamente a acoplar los péndulos se igualaron sus períodos, [math]\displaystyle{ \tau_i }[/math], ajustando las longitudes. Para ello se tomó el péndulo 1 como referencia y se lo hizo oscilar junto a cada uno de los otros, hasta que no se notaran diferencias apreciables en la fase de los movimientos después de 50 períodos. Para determinar la incerteza de medición se midió el tiempo de 100 períodos 5 veces para el péndulo 1, obteniéndose que la desviación estándard para cada medición de 100 períodos era de 0.03 s. A continuación se midieron 100 períodos 1 sola vez para cada uno de los otros 3 péndulos. Los resultados obtenidos son: [math]\displaystyle{ \tau_1 = (1.8851 \pm 0.0003) s \ }[/math], [math]\displaystyle{ f_1 = (0.5305 \pm 0.0001) Hz }[/math] [math]\displaystyle{ \tau_2 = (1.8890 \pm 0.0003) s \ }[/math], [math]\displaystyle{ f_2 = (0.5294 \pm 0.0001) Hz }[/math] [math]\displaystyle{ \tau_3 = (1.8860 \pm 0.0003) s \ }[/math], [math]\displaystyle{ f_3 = (0.5302 \pm 0.0001) Hz }[/math] [math]\displaystyle{ \tau_4 = (1.8884 \pm 0.0003) s \ }[/math], [math]\displaystyle{ f_4 = (0.5295 \pm 0.0001) Hz }[/math]

Los modos normales de este sistema se pueden calcular de manera relativamente simple. Puede ver los cálculos aquí

Numerando los péndulos en orden antihorario empezando por el de abajo en los videos, y usando las coordenadas radiales de cada uno de ellos, los modos normales son: [math]\displaystyle{ u_S = \frac 1 {\sqrt 4} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} }[/math], [math]\displaystyle{ u_X = \frac 1 {\sqrt 2} \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} }[/math], [math]\displaystyle{ u_Y = \frac 1 {\sqrt 2} \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} }[/math], [math]\displaystyle{ u_{AS} = \frac 1 {\sqrt 4} \begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \end{pmatrix} }[/math]

A continuación se muestran los videos y los valores medidos para período y frecuencia de cada uno de ellos

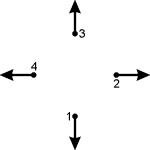
[math]\displaystyle{ u_S = \frac 1 {\sqrt 4} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} }[/math] (modo simétrico)			[math]\displaystyle{ \tau_S = (1.6222 \pm 0.0003) s }[/math] [math]\displaystyle{ f_S = (0.6164 \pm 0.0001) Hz }[/math]
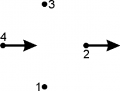
[math]\displaystyle{ u_X = \frac 1 {\sqrt 2} \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} }[/math] (modo X péndulos 2 y 4)			[math]\displaystyle{ \tau_X = (1.7409 \pm 0.0003) s }[/math] [math]\displaystyle{ f_X = (0.5744 \pm 0.0001) Hz }[/math]
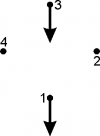
[math]\displaystyle{ u_Y = \frac 1 {\sqrt 2} \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} }[/math] (modo Y péndulos 1 y 3)			[math]\displaystyle{ \tau_Y = (1.7266 \pm 0.0003) s }[/math] [math]\displaystyle{ f_Y = (0.5792 \pm 0.0001) Hz }[/math]
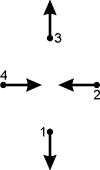
[math]\displaystyle{ u_{AS} = \frac 1 {\sqrt 2} \begin{pmatrix} 1 \\ -1 \\ 1 \\ -1 \end{pmatrix} }[/math] (modo antisimétrico)			[math]\displaystyle{ \tau_{AS} = (1.8540 \pm 0.0003) s }[/math] [math]\displaystyle{ f_{AS} = (0.5394 \pm 0.0001) Hz }[/math]

Cualquier movimiento del sistema se puede expresar como una superposición de movimientos de estos modos normales. Por ejemplo, si iniciamos el movimiento sosteniendo los péndulos 1 y 3 hacia afuera con igual desplazamiento, la condición inicial del sistema es [math]\displaystyle{ u(0) = \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \end{pmatrix} }[/math], que puede ser escrita como [math]\displaystyle{ u(0) = \sqrt 4 \, \left[ u_S(0) + u_{AS}(0) \right] }[/math]. Como la frecuencia de los modos [math]\displaystyle{ u_S }[/math] y [math]\displaystyle{ u_{AS} }[/math] son distintas, al evolucionar en el tiempo aparecerá un "batido" entre ambas frecuencias.

En el video se observa claramente este "batido" cuando el movimiento se traslada de los péndulos 1-3 a los 2-4 ida y vuelta. El período de esta ida y vuelta se midió en [math]\displaystyle{ \tau_B = 12.76 s }[/math], indicando una frecuencia de [math]\displaystyle{ f_B = 0.0784 Hz }[/math]. Este valor coincide muy aproximadamente con [math]\displaystyle{ f_S - f_{AS} = 0.0770 Hz }[/math]

Algo similar ocurre con la condición inicial [math]\displaystyle{ u(0) = \begin{pmatrix} 0 \\ -1 \\ 2 \\ -1 \end{pmatrix} }[/math] que corresponde a acercar los pendulos en la dirección X al centro en igual cantidad y alejar el péndulo 3 en la dirección Y el doble. Esto puede ser descripto como [math]\displaystyle{ u(0) = \sqrt 4 \, u_{AS}(0) - \sqrt 2 \, u_Y(0) }[/math].

Aquí también se observa un batido con transferencia de movimiento entre los péndulos 1 y 3 mientras los 2-4 se mantienen moviendo constantemente. El período de esta ida y vuelta se midió en [math]\displaystyle{ \tau_B = 25.04 s }[/math], indicando una frecuencia de [math]\displaystyle{ f_B = 0.0399 Hz }[/math]. Este valor coincide muy aproximadamente con [math]\displaystyle{ f_Y - f_{AS} = 0.0398 Hz }[/math]